Quantitations

Expected Number of Steps of a Markov Process Math, CS, Data

$\newcommand{\E}{\mathbb{E}}\newcommand{\I}{\mathbb{I}}\renewcommand{\P}{\mathbb{P}}$

If we want to find the expected number of steps until “completion” of a Markov process, often we can use conditioning to get a sufficient system of equations. Each state provides one equation. Let $T_{S_i}$ be a random variable corresponding to the number of steps required to reach completion, starting from state $S_i$. Finally, let $p_{i,j}$ be the transition probability from $S_i$ to $S_j$.

\begin{align*} \E [ T_{S_i} ] &= \sum_j p_{i,j} \E [ T_{S_i} \vert \text{next state is } S_j]\\ &= \sum_j p_{i,j} \E [ 1 + T_{S_j} \vert \text{next state is } S_j]\\ &= 1 + \sum_j p_{i,j} \E [ T_{S_j} ] \end{align*}

Example

Here’s an example of this technique. This question comes from an old qualifying exam:

Hidden inside each box of Primate brand breakfast cereal is a small plastic figure of an animal: an ape, a baboon, or a chimp. Suppose a fraction $\alpha$ of the very large population of cereal boxes contain apes, a fraction $\beta$ contain baboons, and a fraction $\gamma$ contain chimps. Find the expected number of boxes you need to buy before you have at least one figure of each type.

The situation can be modelled by a Markov process corresponding to the following diagram. $S$ represents the starting state. To simplify the picture, arrows from a state to itself are not drawn but are implied to account for any “missing” probability.

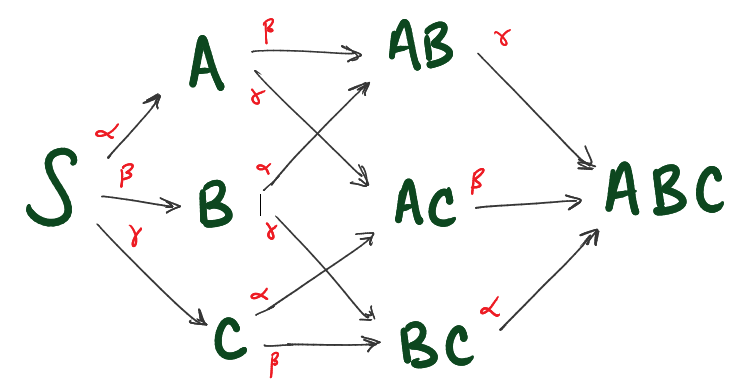
markov diagram

Let $E_X(Y)$ denote the expected number of transitions required to reach state $Y$ from state $X$. Our goal is to find $E_S(ABC)$. By looking at the diagram and conditioning on the next step, we can derive the following recurrence relationships.

\begin{align*} E_S(ABC) &= 1 + \alpha E_A(ABC) + \beta E_B(ABC) + \gamma E_C(ABC)\\ E_A(ABC) &= 1 + \alpha E_A(ABC) + \beta E_{AB}(ABC) + \gamma E_{AC}(ABC)\\ E_B(ABC) &= 1 + \beta E_B(ABC) + \alpha E_{AB}(ABC) + \gamma E_{BC}(ABC)\\ E_C(ABC) &= 1 + \gamma E_C(ABC) + \alpha E_{AC}(ABC) + \beta E_{BC}(ABC) \end{align*}

And by recognizing that the final transition to $ABC$ is a Geometric process, we realize that

\begin{align*} E_{AB}(ABC) = \frac{1}{\gamma} \qquad \qquad E_{AC}(ABC) = \frac{1}{\beta} \qquad \qquad E_{BC}(ABC) = \frac{1}{\alpha} \end{align*}

Putting it all together,

\begin{align*} E_S(ABC) = 1 + \frac{\alpha}{1-\alpha}\left(1 + \frac{\beta}{\gamma} + \frac{\gamma}{\beta}\right) + \frac{\beta}{1-\beta}\left(1 + \frac{\alpha}{\gamma} + \frac{\gamma}{\alpha}\right) + \frac{\gamma}{1-\gamma}\left(1 + \frac{\alpha}{\beta} + \frac{\beta}{\alpha}\right) \end{align*}
blog comments powered by Disqus

Published

07 February 2013

Tags