Numerical Derivatives in R Math, CS, Data
I was recently trying to compute a second derivative numerically in R, and I had some trouble finding a simple built-in function for the task. deriv takes expressions and finds symbolic derivatives. numericDeriv also uses takes expressions, and only finds the first derivative. I wrote a simpler derivative function that finds numerical derivatives with respect to a single variable.
derivative <- function(f, x, ..., order = 1, delta = 0.1, sig = 6) {
# Numerically computes the specified order derivative of f at x
vals <- matrix(NA, nrow = order + 1, ncol = order + 1)
grid <- seq(x - delta/2, x + delta/2, length.out = order + 1)
vals[1, ] <- sapply(grid, f, ...) - f(x, ...)
for (i in 2:(order + 1)) {
for (j in 1:(order - i + 2)) {
stepsize <- grid[i + j - 1] - grid[i + j - 2]
vals[i, j] <- (vals[i - 1, j + 1] - vals[i - 1, j])/stepsize
}
}
return(signif(vals[order + 1, 1], sig))
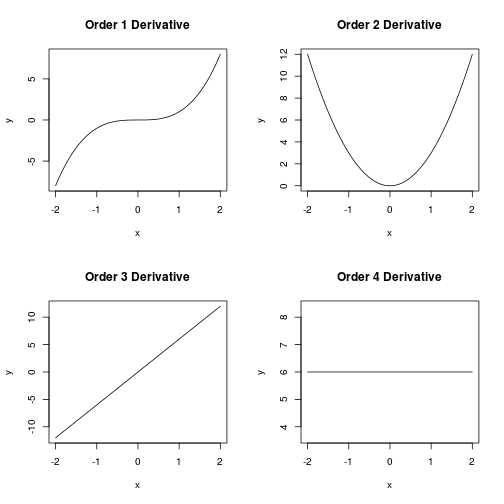
}In the following example, we find and plot the first four derivatives of $x^4/4$ on a grid over the interval $[-5, 5]$.
g <- function(x) {
return(x^4/4)
}
par(mfrow = c(2, 2))
grid <- seq(-2, 2, by = 0.01)
for (i in 1:4) {
plot(grid, sapply(grid, derivative, f = g, order = i), type = "l", xlab = "x",
ylab = "y", main = paste("Order", i, "Derivative"))
}
Be careful when you’re taking higher derivatives; the round-off error can really add up. You may have to tune delta and sig to improve its performance.
blog comments powered by Disqus